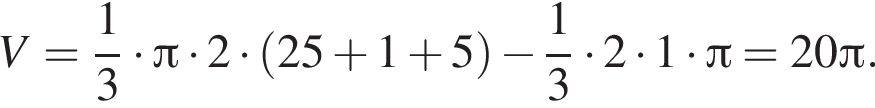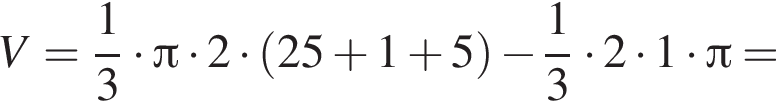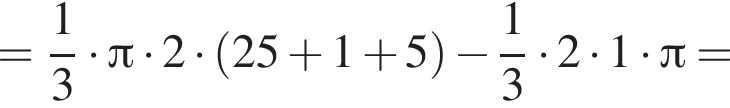Укажите номер рисунка, на котором изображены фигуры, симметричные относительно прямой l.
Длины катетов прямоугольного треугольника являются корнями уравнения x2 − 9x + 6 = 0. Найдите площадь треугольника.
На рисунке две прямые пересекаются в точке О. Если
 то угол AOD равен:
то угол AOD равен:
Укажите номер выражения, являющегося одночленом восьмой степени:
а) 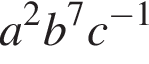 | б) 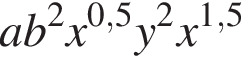 | в) | г) 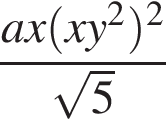 | д) |
От пристани одновременно отправляются по течению реки катер(I) и против течения реки моторная лодка (II). На рисунке приведены графики их движения. Определите скорость течения реки (в км/ч), если катер и моторная лодка имеют одинаковые собственные скорости.
Значение выражения 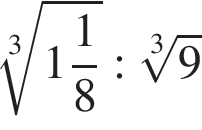 равно:
равно:
На координатной плоскости изображен тупоугольный треугольник ABC с вершинами в узлах сетки (см. рис.). Косинус угла ABC этого треугольника равен:
Значение выражения 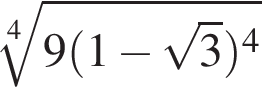 равно:
равно:
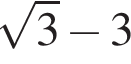
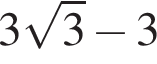
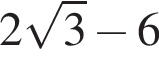
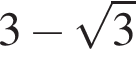
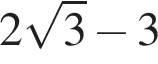
Упростите выражение  если
если ![]()
![]()
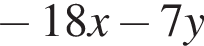
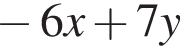

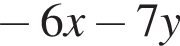

Функция y = f(x) определена на множестве действительных чисел. Известно, что 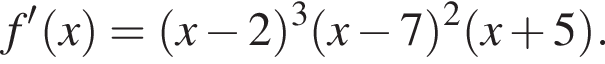 Найдите произведение точек экстремума функции y = f(x).
Найдите произведение точек экстремума функции y = f(x).
Автомобиль проехал некоторое расстояние, израсходовав 15 л топлива. Расход топлива при этом составил 9 л на 100 км пробега. Затем автомобиль существенно увеличил скорость, в результате чего расход топлива вырос до 12 л на 100 км. Сколько литров топлива понадобится автомобилю, чтобы проехать такое же расстояние?
Найдите произведение большего корня на количество корней уравнения 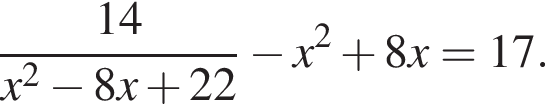
Найдите модуль разности наибольшего и наименьшего корней уравнения 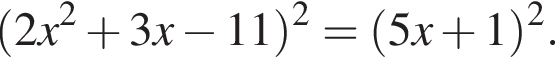
Найдите периметр правильного шестиугольника, меньшая диагональ которого равна ![]()
Выберите все верные утверждения, являющиеся свойствами нечетной функции ![]() определённой на
определённой на  и заданной формулой
и заданной формулой 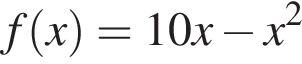 при
при ![]()
1. Функция имеет три нуля.
2. Функция убывает на промежутке [−8; −6].
3. Минимум функции равен −25.
4. Максимальное значение функции равно 25.
5. 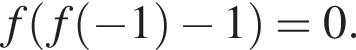
6. Функция принимает отрицательные значения при 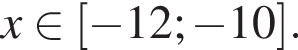
7. График функции симметричен относительно оси абсцисс.
Ответ запишите в виде последовательности цифр в порядке возрастания. Например: 123.
Найдите сумму (в градусах) наименьшего положительного и наибольшего отрицательного корней уравнения 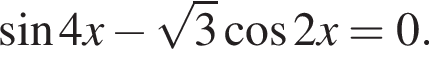
Найдите сумму корней уравнения
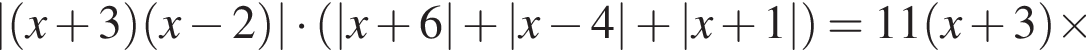
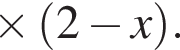
Найдите наибольшее целое решение неравенства 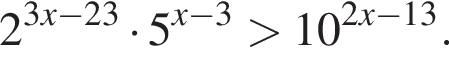
На пастбище квадратной формы загон для скота огорожен так, как показано на рисунке. Все размеры указаны в метрах. Найдите площадь загона (в м2), если площадь пастбища в 72 раза больше площади загона.
Найдите значение выражения 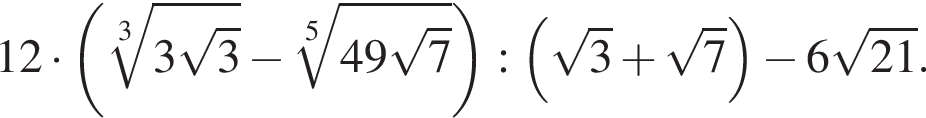
В равнобокой трапеции большее основание вдвое больше каждой из остальных сторон и лежит в плоскости α. Боковая сторона образует с плоскостью α угол, синус которого равен ![]() Найдите 36sinβ, где β — угол между диагональю трапеции и плоскостью α.
Найдите 36sinβ, где β — угол между диагональю трапеции и плоскостью α.
Найдите произведение корней (корень, если он единственный) уравнения 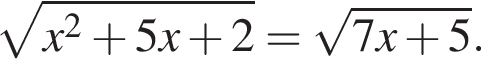
Найдите значение выражения 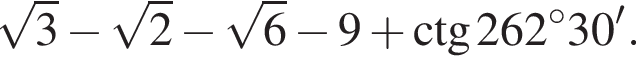
Куб вписан в правильную четырехугольную пирамиду так, что четыре его вершины находятся на боковых ребрах пирамиды, а четыре другие вершины — на ее основании. Длина стороны основания пирамиды равна 1, высота пирамиды — 2. Найдите площадь S поверхности куба. В ответ запишите значение выражения 3S.
О натуральных числах а и b известно, что 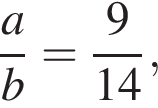 НОД(a; b) = 5. Найдите НОК(a + b; 10).
НОД(a; b) = 5. Найдите НОК(a + b; 10).
Найдите значение выражения 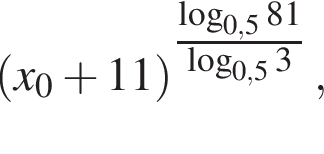 где x0 — корень уравнения
где x0 — корень уравнения 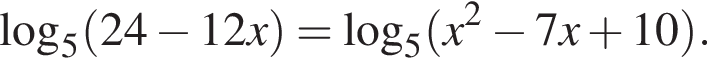
Значение выражения 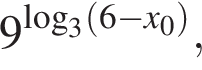 где x0 — корень уравнения
где x0 — корень уравнения 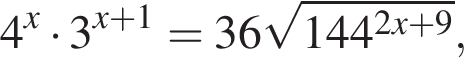 равно ... .
равно ... .
Найдите все пары (m, n) целых чисел, которые связаны соотношением m2 + 4m = n2 − 2n + 8. Пусть k — количество таких пар, m0 — наименьшее из значений m, тогда значение выражения k · m0 равно ... .
На стороне AB параллелограмма ABCD отмечена точка O так, что 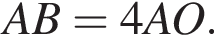 К плоскости ABCD из точки O восстановлен перпендикуляр SO длиной 5. Найдите значение выражения
К плоскости ABCD из точки O восстановлен перпендикуляр SO длиной 5. Найдите значение выражения 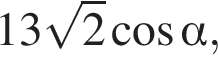 где
где ![]() — линейный угол двугранного угла BSCD, если
— линейный угол двугранного угла BSCD, если 
 и известно, что площадь ABCD равна 80.
и известно, что площадь ABCD равна 80.
Прямоугольный треугольник, длина гипотенузы которого равна 5, высота, проведенная к ней равна 2, вращается вокруг прямой, перпендикулярной гипотенузе и проходящей в плоскости треугольника через вершину большего острого угла. Найдите объем V тела вращения и в ответ запишите значение выражения ![]()

 равна 360°, поэтому
равна 360°, поэтому 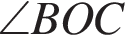 равен 70°. Углы
равен 70°. Углы 
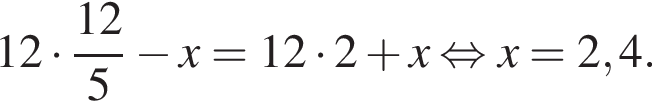
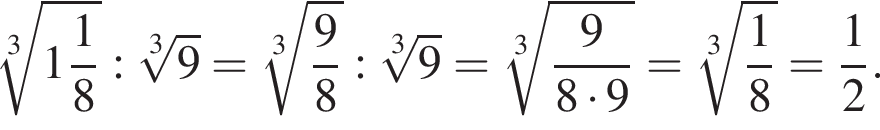
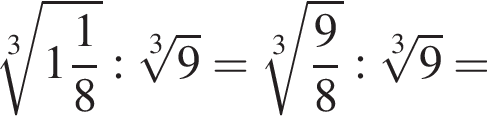
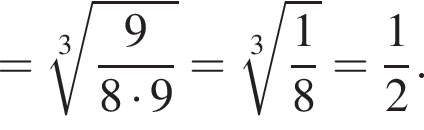
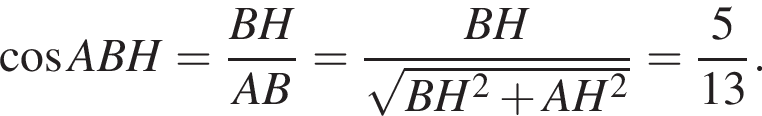
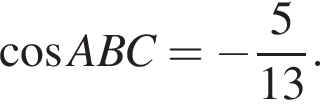
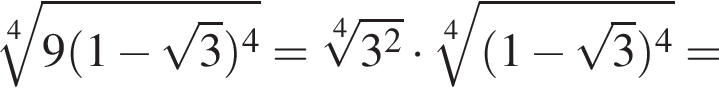
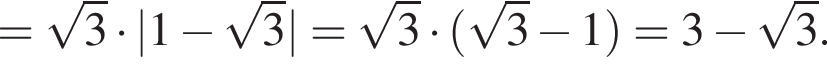
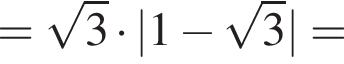
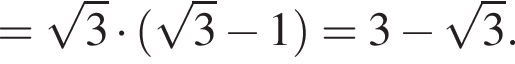
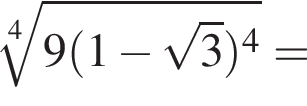
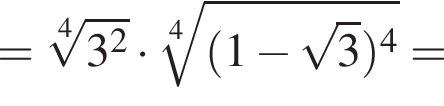
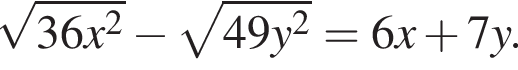
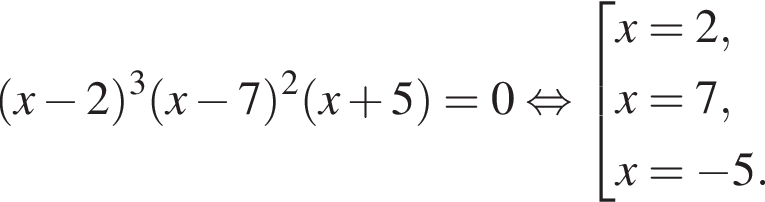
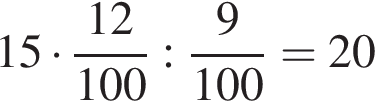 л.
л.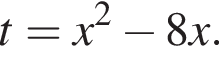 Тогда:
Тогда: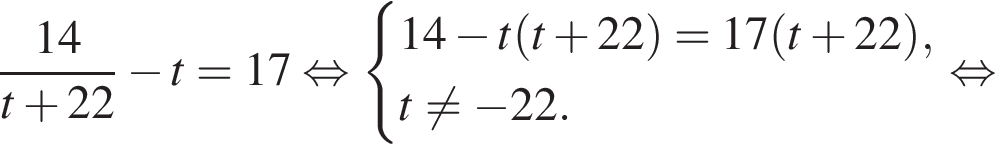
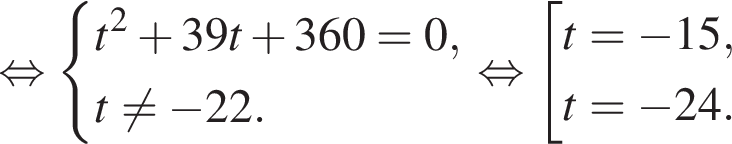
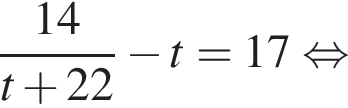
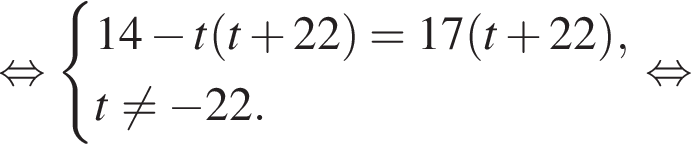
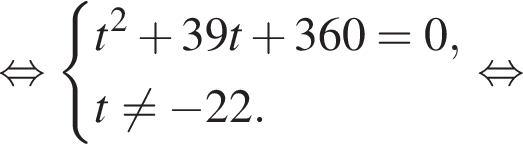
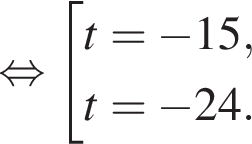
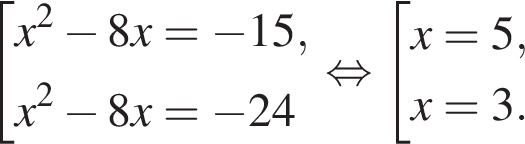
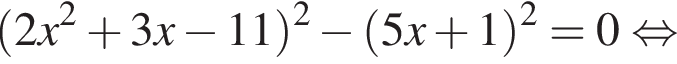
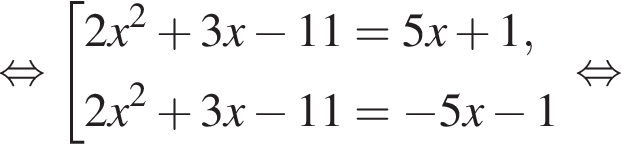
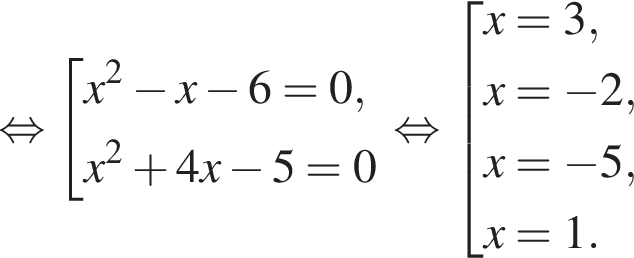
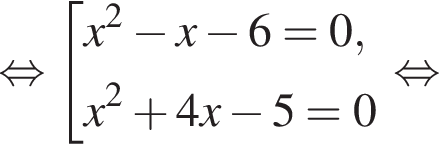
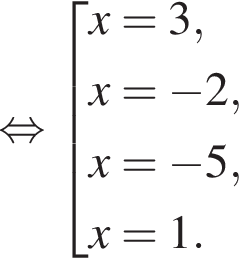
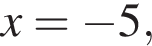 модуль разности наибольшего и наименьшего корней уравнения равен 8.
модуль разности наибольшего и наименьшего корней уравнения равен 8.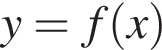 при
при  Утверждение 2 верно.
Утверждение 2 верно. значит, ее максимальное значение не может быть равно −25.
значит, ее максимальное значение не может быть равно −25.
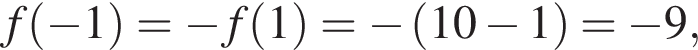 поэтому
поэтому 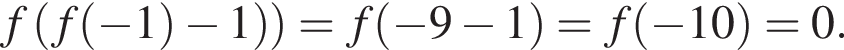
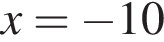 функция равна нулю, а значит, принимает отрицательные значения не во всех точках отрезка
функция равна нулю, а значит, принимает отрицательные значения не во всех точках отрезка 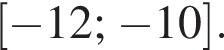 Утверждение 6 неверно.
Утверждение 6 неверно.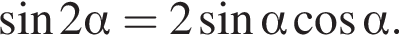 Тогда:
Тогда:
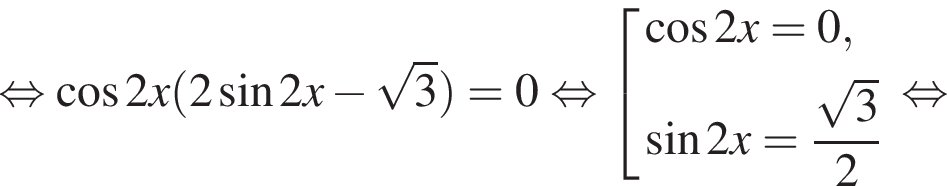
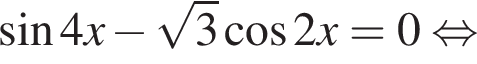

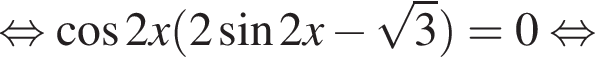
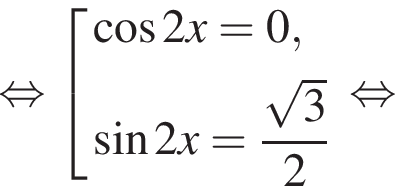
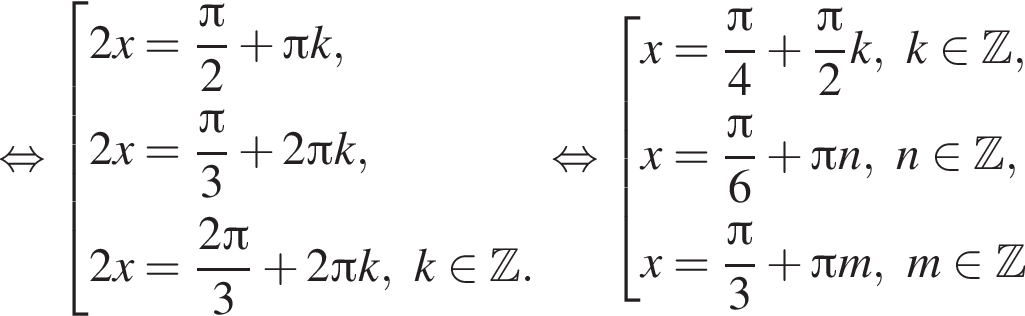
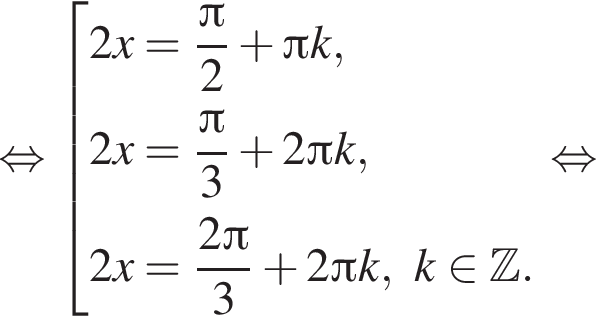
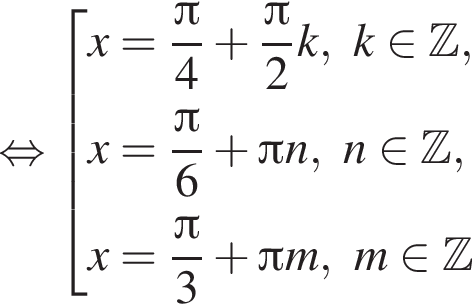
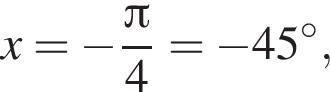 наименьшим положительным решением уравнения является корень
наименьшим положительным решением уравнения является корень 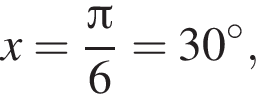 их сумма равна −15°.
их сумма равна −15°.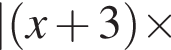
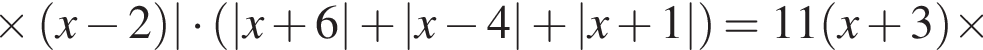
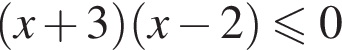 :
: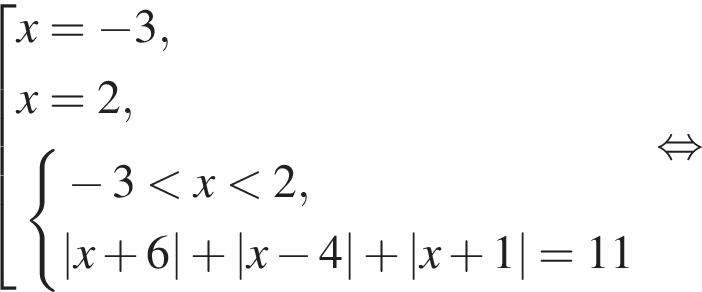
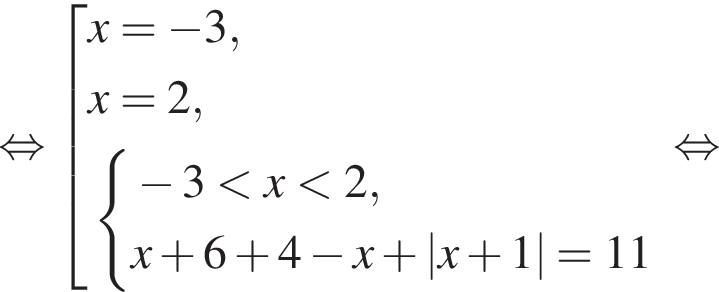
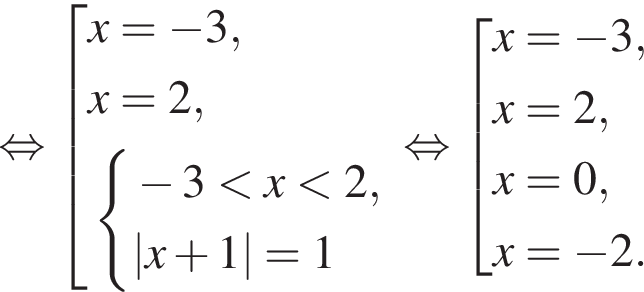
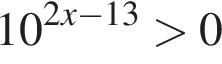 :
: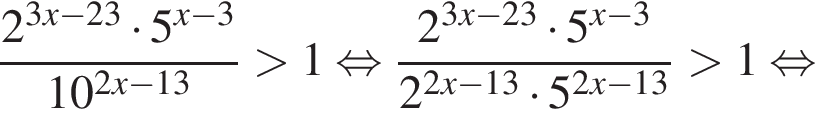
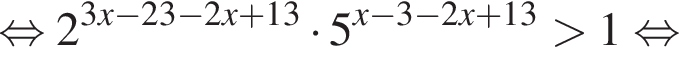
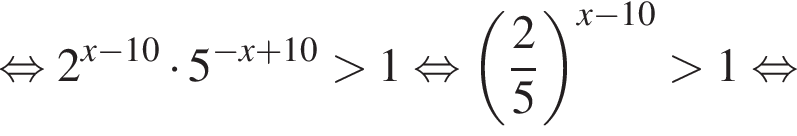
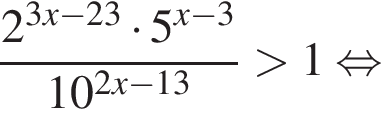
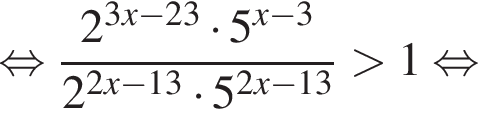
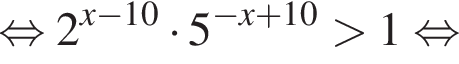
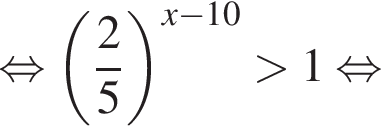

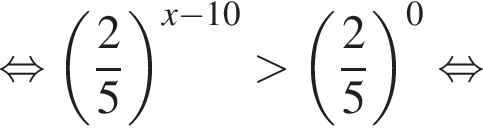
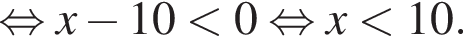
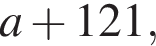 т. е.
т. е. 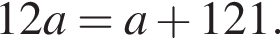 Откуда
Откуда 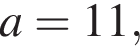 а площадь загона равна
а площадь загона равна 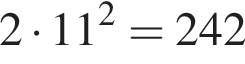 м2.
м2.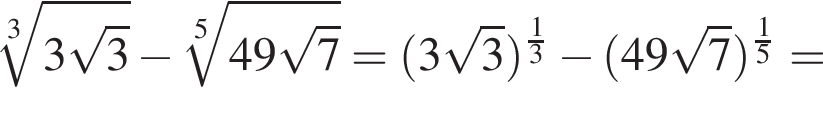
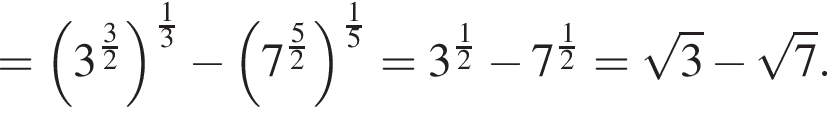
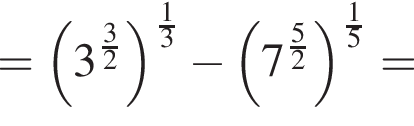
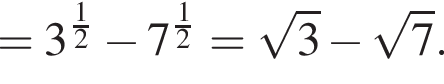
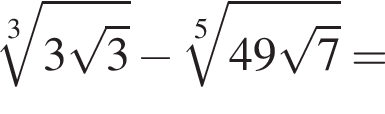
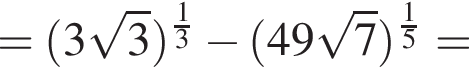
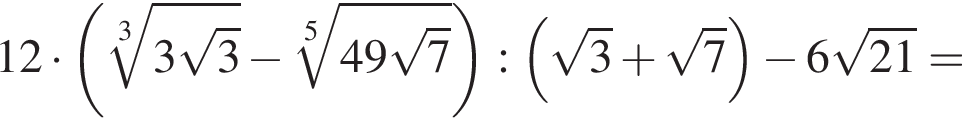
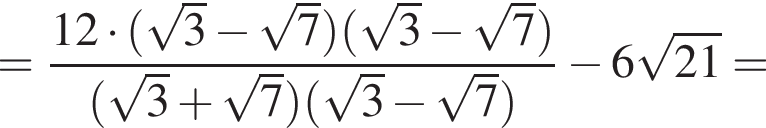
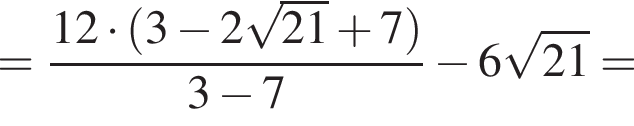
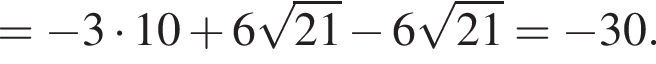

 Поскольку все стороны трапеции, кроме большего основания равны a, получим
Поскольку все стороны трапеции, кроме большего основания равны a, получим  Тогда
Тогда 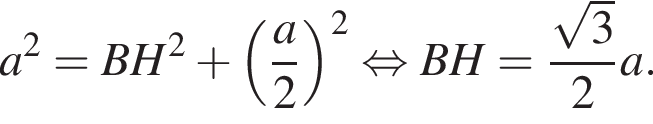

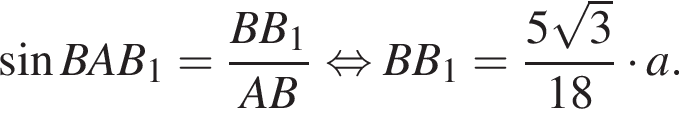
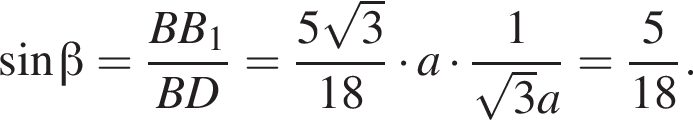
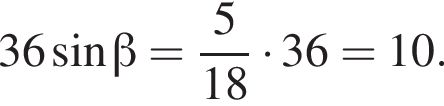
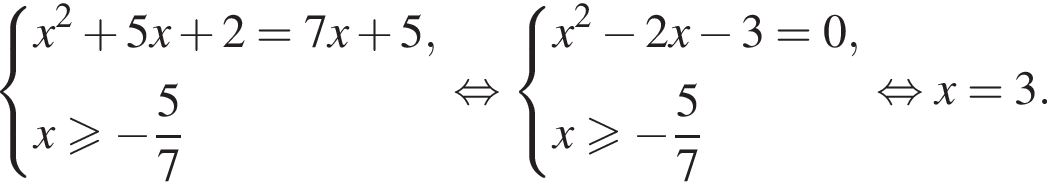
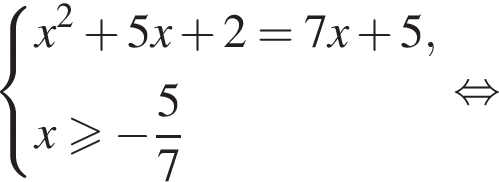
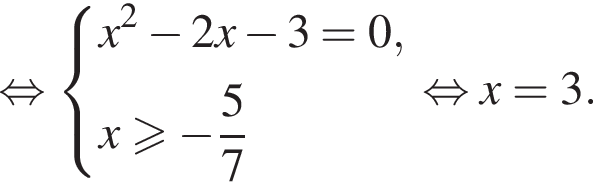

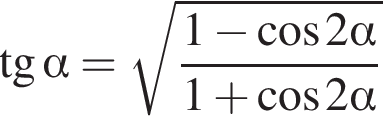 :
: 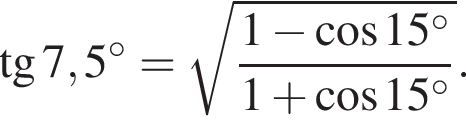



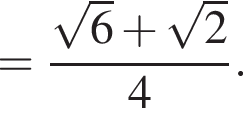
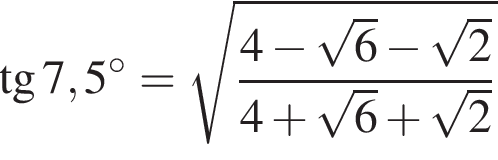
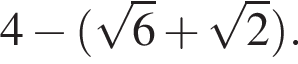 Тогда:
Тогда: 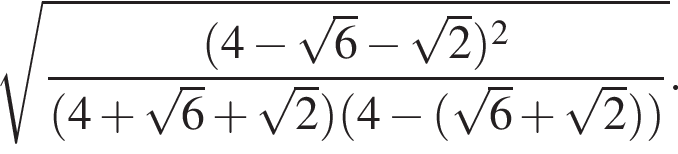
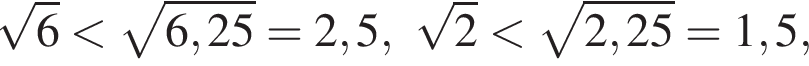
 тогда
тогда 
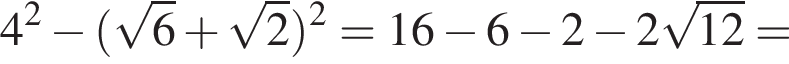

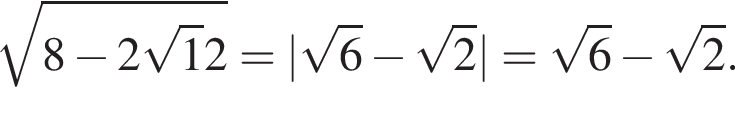 Тогда:
Тогда: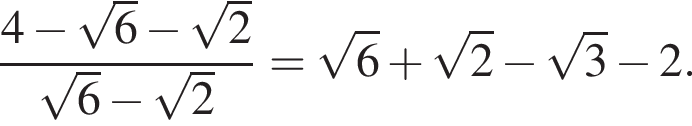
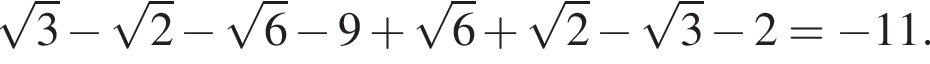
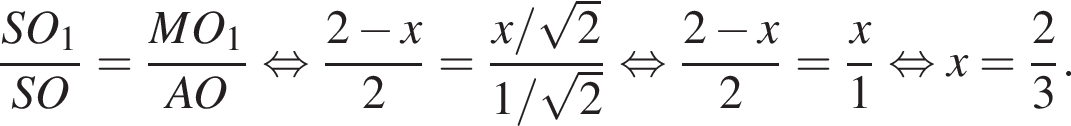
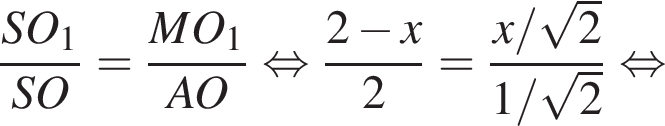
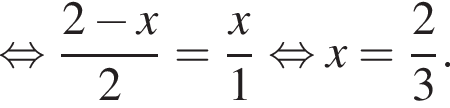
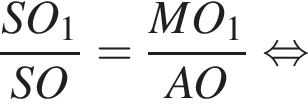
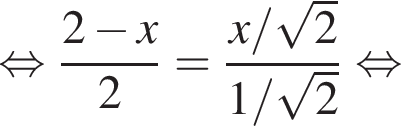
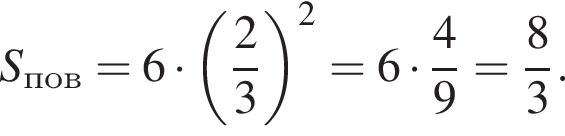
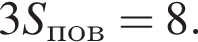
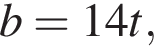 тогда
тогда  откуда
откуда 
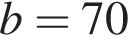 и
и 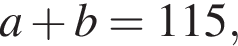 тогда искомое наименьшее общее кратное равно
тогда искомое наименьшее общее кратное равно 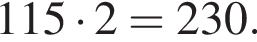
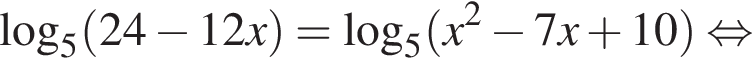
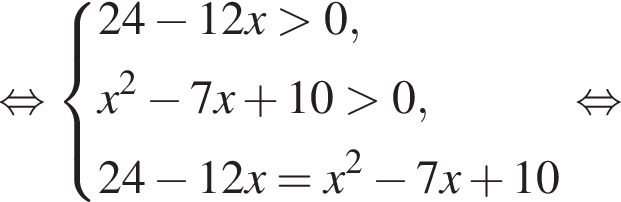
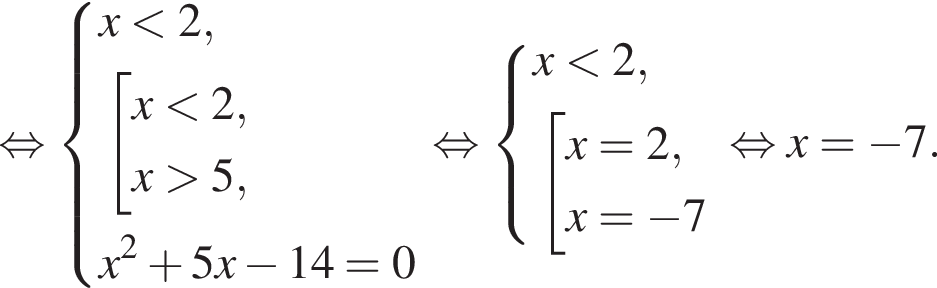
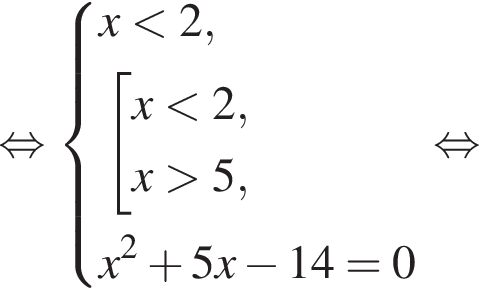
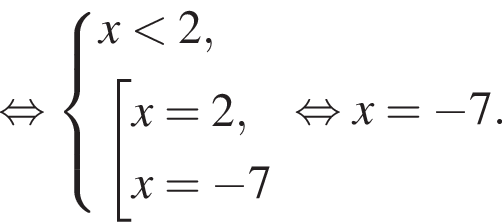
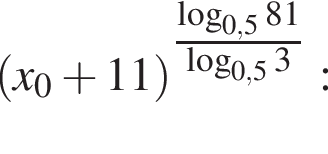
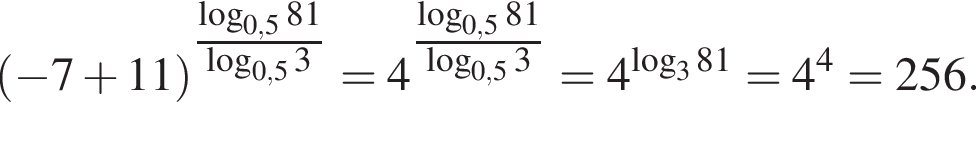
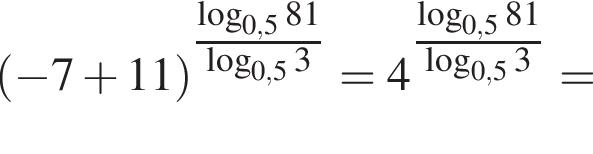


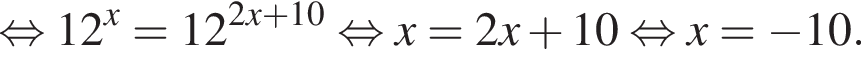
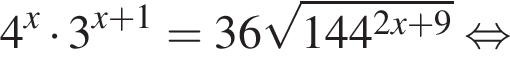
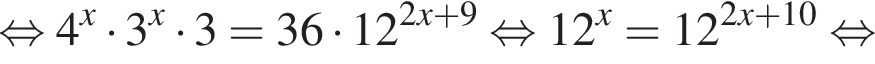
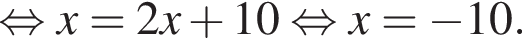
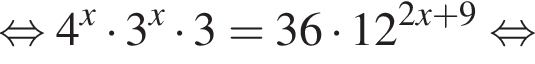
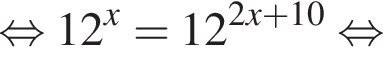
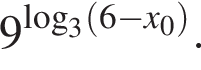 Получаем:
Получаем: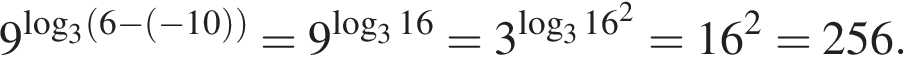
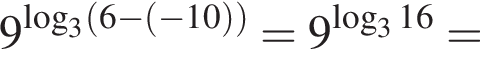
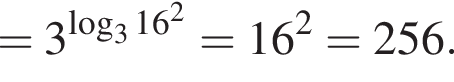
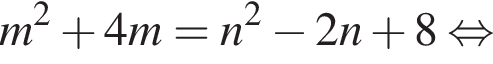
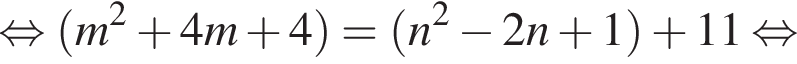
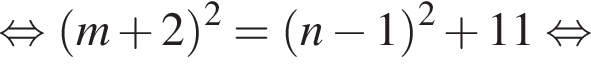
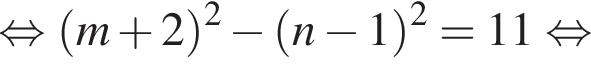
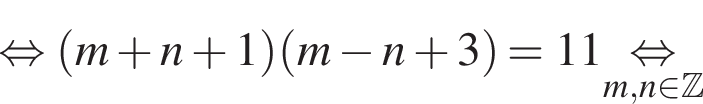
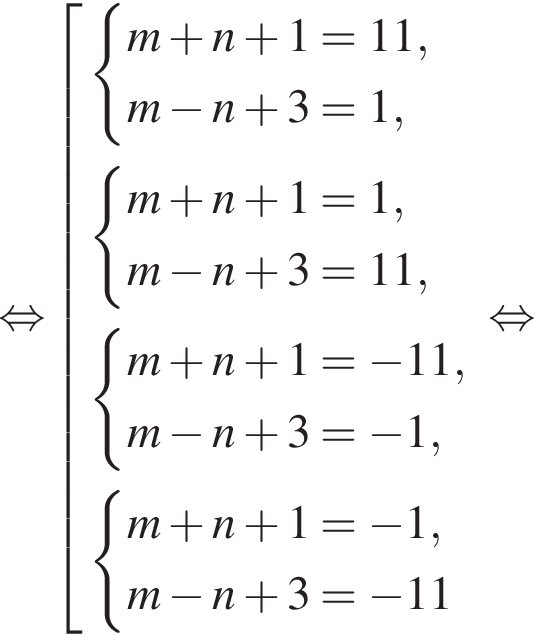
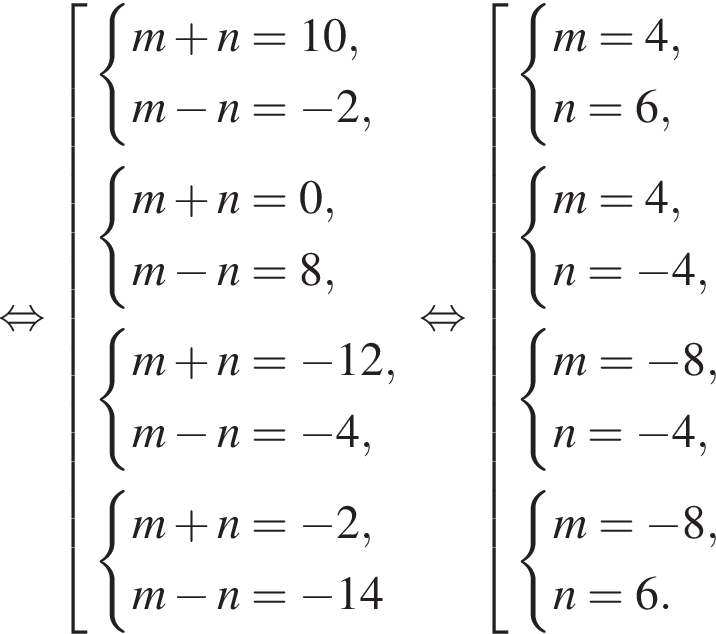
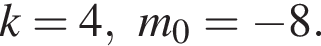 Получаем
Получаем 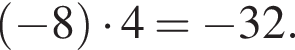
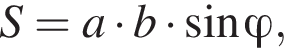 где a и b стороны параллелограмма, а
где a и b стороны параллелограмма, а  а параллелограмм ABCD является прямоугольником. По теореме Пифагора:
а параллелограмм ABCD является прямоугольником. По теореме Пифагора:


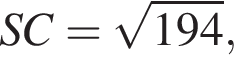
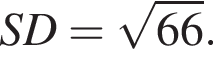

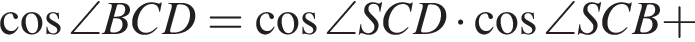

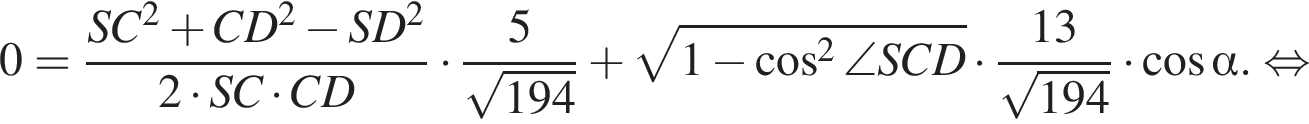
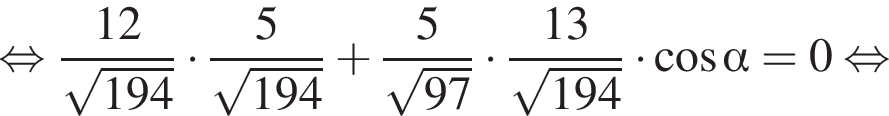
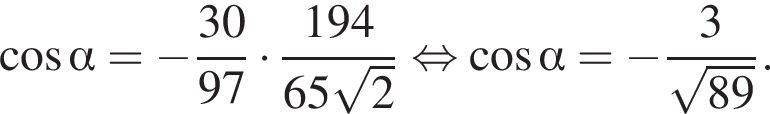
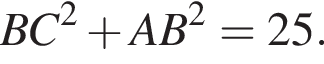 Площадь треугольника, с одной стороны, равна половине произведения катетов, а с другой — половина произведения высоты на сторону, к которой проведена высота. Имеем:
Площадь треугольника, с одной стороны, равна половине произведения катетов, а с другой — половина произведения высоты на сторону, к которой проведена высота. Имеем: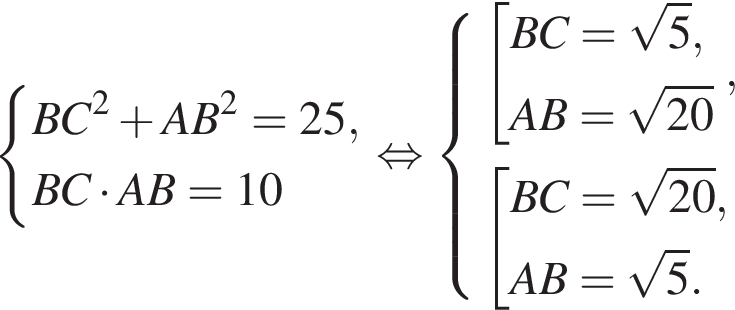
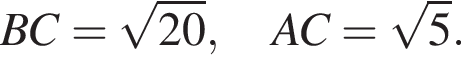 По теореме Пифагора найдем
По теореме Пифагора найдем